关于勾股定理的历史及其证明方法

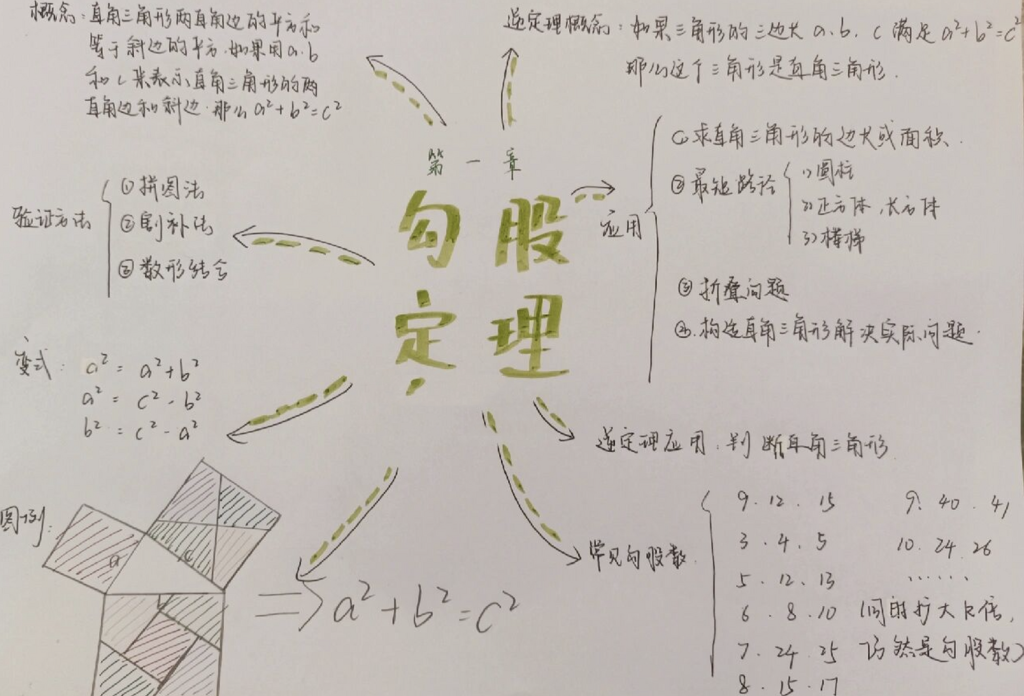
一、勾股定理的历史

勾股定理是古希腊数学家毕达哥拉斯提出的，他发现了直角三角形中的一个重要关系。据说，毕达哥拉斯是在观察埃及的金字塔时发现了这个定理。他将这个定理命名为“勾股定理”，以纪念他的学生勾股。

二、勾股定理的证明方法

勾股定理有多种证明方法，其中最著名的是几何证明和代数证明。几何证明通过构造图形和运用几何性质来证明定理的正确性，而代数证明则通过代数运算和方程推导来证明。这些证明方法都有其独特的思路和步骤，可以帮助学生更好地理解和掌握勾股定理。

三、勾股定理的应用领域

勾股定理在几何学中有广泛的应用。它可以用来计算三角形的边长和角度，判断三角形的形状，解决与三角形相关的问题等。此外，勾股定理还可以应用于物理学、工程学等领域，用来解决实际问题。

四、勾股定理的推广

勾股定理不仅适用于直角三角形，还可以推广到其他类型的三角形。例如，钝角三角形和锐角三角形也可以应用勾股定理来计算边长和角度。这种推广可以帮助学生更深入地理解勾股定理的原理和应用。

五、勾股定理的实际问题

勾股定理在实际生活中有很多应用。例如，可以用勾股定理来计算建筑物的高度、测量地面的距离、解决航海和航空导航中的问题等。这些实际问题可以激发学生对勾股定理的兴趣，并将其应用于实际情境中。

六、勾股定理的教学策略

在教学勾股定理时，可以采用多种策略来帮助学生理解和掌握。例如，可以通过实际测量和实验来验证勾股定理，让学生亲自体验定理的正确性。此外，还可以通过解决实际问题和进行探究活动来培养学生的问题解决能力和创新思维。